- ellipsoïde
-
ellipsoïde [ elipsɔid ] n. m. et adj.• 1705; de 2. ellipse et -oïde♦ Math.1 ♦ Quadrique dont les sections planes sont des ellipses. Ellipsoïde de révolution : solide engendré par une ellipse tournant autour d'un de ses axes (allongé, autour du grand axe; aplati, autour du petit). En forme d'ellipsoïde (ELLIPSOÏDAL, ALE, AUX adj. ).— Géogr. Ellipsoïde de référence : ellipsoïde de révolution aplati, d'axe parallèle à la ligne des pôles, utilisé en cartographie.2 ♦ Adj. (1845) Qui a la forme d'une ellipse. ⇒ 2. elliptique.
● ellipsoïde nom masculin Quadrique dont une équation est de la forme ● ellipsoïde (expressions) nom masculin Ellipsoïde de révolution, ellipsoïde dont une équation est
, avec a = b ≠ c. (Son volume intérieur est égal à 
).
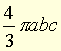Ellipsoïde terrestre, ellipsoïde de révolution aplati dont le petit axe est parallèle à l'axe du monde et que les géodésiens utilisent pour le calcul des coordonnées géographiques.
ellipsoïden. m. et adj.d1./d n. m. GEOM Surface fermée dont le cône directeur est imaginaire et dont toute section est une ellipse. Ellipsoïde de révolution: solide engendré par la révolution d'une ellipse autour de l'un de ses axes.d2./d adj. Qui a la forme d'une ellipse.⇒ELLIPSOÏDE, adj. et subst. masc.I.— Adj. Qui a la forme d'une ellipse ou une forme approchante (cf. ellipse2). Les argiles plastiques se présentent ordinairement en amas à peu près lenticulaires et ellipsoïdes (A. BRONGNIART, Arts céram., 1844, p. 64). Des tondeurs taillaient les arbres et leur donnaient une forme ronde ou ellipsoïde (GAUTIER, Rom. momie, 1858, p. 242).II.— Subst. masc., GÉOM. Surface à trois dimensions dont toutes les sections planes sont des ellipses.— En partic. Ellipsoïde (de révolution). Surface engendrée par la rotation d'une ellipse autour de l'un de ses axes. Un ellipsoïde de révolution peu différent d'une sphère (POINCARÉ, Hyp. cosmogon., 1911, p. 188).Prononc. et Orth. :[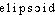
] ou [
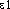(l)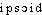
]. Ds Ac. dep. 1835. Étymol. et Hist. [1705 géom. d'apr. BL.-W.3-5]; 1721 (Hist. Acad. Sc., p. 46 ds DG). Dér. de ellipse; suff. -oïde. Fréq. abs. littér. :9.DÉR. 1. Ellipsoïdal, ale, aux, adj. Qui a la forme d'un ellipsoïde ou une forme approchante. L'excès de l'altitude des mâts et des voiles (...) menace de coucher sur le flanc le vaisseau, dont la forme ellipsoïdale rend le roulis inévitable et parfois compromettant (MAIZIÈRE, Nouv. archit. nav., 1853, p. 57). Les figures ellipsoïdales en rotation deviennent instables lorsque leur aplatissement devient très grand (SCHATZMAN, Astrophys., 1963, p. 139). — [
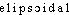], [-o]. — 1re attest. 1845 (BESCH.); de ellipsoïde, suff. -al. — Fréq. abs. littér. : 1. 2. Ellipsoïdique, adj. Relatif à un ellipsoïde. Assurer pour tout point la correspondance entre ses coordonnées astronomiques et des coordonnées ellipsoïdiques se référant à un ellipsoïde de référence unique pour l'ensemble de la terre (Hist. gén. sc., t. 3, vol. 2, 1964, p. 457). — [
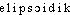] (Lar. Lang. fr.). — 1re attest. 1964 surface, coordonnées ellipsoïdique(s) (Hist. gén. sc., t. 3, vol. 2, p. 456 et 457); de ellipsoïde, suff. -ique.ellipsoïde [elipsɔid] n. m. et adj.ÉTYM. 1705; de 2. ellipse, et -oïde.❖♦ Didactique (géométrie).———I N. m. Surface quadrique dont les sections planes sont des ellipses. || Ellipsoïde de révolution : ellipsoïde engendré par une ellipse tournant autour d'un de ses axes (allongé, autour du grand axe; aplati, autour du petit axe). || La sphère est un ellipsoïde de révolution particulier, engendré par un cercle. || La forme normale d'un corps fluide en rotation est un ellipsoïde de révolution. || Aplatissement d'un ellipsoïde de révolution (planète, etc.). || La Terre peut se représenter par un ellipsoïde de révolution aplati aux pôles. ⇒ Géoïde. || En forme d'ellipsoïde. ⇒ Ellipsoïdal.———II Adj. (1845). Qui a la forme d'une ellipse. ⇒ 2. Elliptique. || Figure ellipsoïde. || Saillie ellipsoïde (→ Condyle, cit. 1).❖DÉR. Ellipsoïdal, ellipsoïdique.
Encyclopédie Universelle. 2012.
